Introduction

The original squash ranking system was fairly simplistic and was just based on the principle that if you beat a player with a better ranking than yourself, then your ranking was improved and your opponents ranking was degraded.  However, if you lost to a player with a better ranking than yourself, then both players rankings remained unchanged.

This system worked reasonably well, however it did tend to pull player rankings together into clumps.

After some investigation on the Internet, the ranking system used by Avon and Bristol District Squash looked impressive and has been adapted for use by Ickleford Squash Club.

Improved System

The new Ickleford Ranking System is based on a logarithmic scale of ability whereby the difference between any two players rankings is a measure of their relative ability as follows:-

Ranking Difference	Relative ability
0	Players are equal ability
20	Player with the lower ranking is 2 times better
40	Player with the lower ranking is 4 times better
60	Player with the lower ranking is 8 times better

 

The following graph shows the assumed probability of winning each point based on the relative ranking.

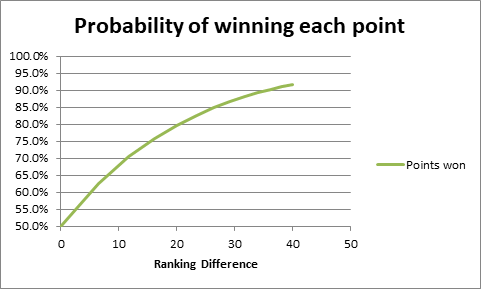
Figure 1

The above graph is largely hypothetical but is very similar to the Avon and Bristol system, which is based on empirical data.  It also accords quite closely with player experience.  Note that two players of the same ranking (zero difference) have a 50% probability each of winning each point.  A player who is twice as good (ranking difference of 20), has approximately an 80% chance of winning each point ie. they will win 4 points out of every 5 on average.  As the ranking difference increases, then the probability of the better player winning each point tends towards 100%, however there is always a chance that the lesser player will sneak the odd point, so the line never reaches 100%.

Assuming that the probability of winning each point shown in Figure 1 is correct, then it is fairly simple to calculate the probability of match results.

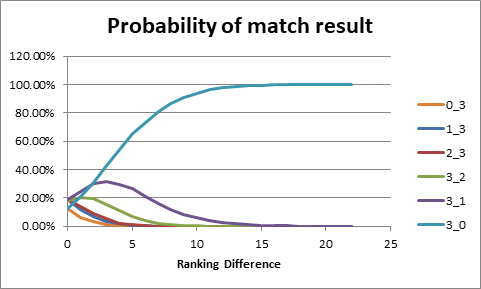
Figure 2

Figure 2 shows the probability of each match result for PAR scoring to 15 points, best of 5 games.  The calculation is based on the simulation of thousands of matches, where the probability of each point is taken from the graph in Figure 1.  It ignores the possibility of any match not reaching a full result due to lack of time.

As might be expected, the probability of a 3-0 win by the better player rises rapidly with increasing ranking difference.  The probability of a 3-0 win is around 60% for a ranking difference of 5, 94% for a ranking difference of 10, and almost 100% for a ranking difference of 15 or more.

Interestingly, the probability of a 3-2 win by the better player never exceeds more than around 20%, and the probability of a 3-1 win by the better play peaks at around 30% for a ranking difference of 3.

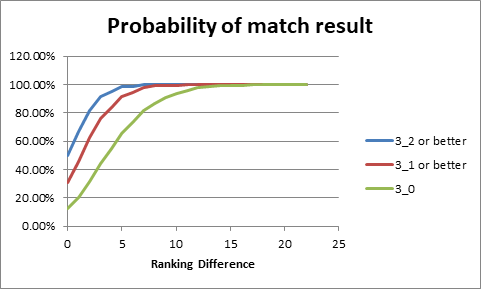
Figure 3

Figure 3 shows the probability of a win by the better player.  This rises even more sharply with increasing ranking difference, reaching almost 100% for a ranking difference of 5 or more.

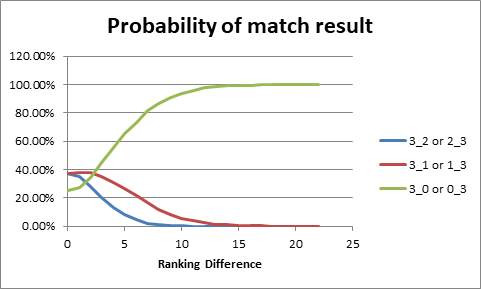
Figure 4

Figure 4 shows the probability of a 3-2, 3-1 and 3-0 wins either way versus ranking difference.  Perhaps surprising, this shows that a match result of 3-1 either way around is the most likely result for ranking differences of approximately 2 or less.

Adjusting Rankings

Based on the previous analysis, the following table shows the most likely ranking difference for each league match result.

Match Score	Likely ranking difference
3-0	5
3-1	3
3-2	1
2-2	0
2-1	1
2-0	1
1-1	0
1-0	1
0-0	0
0-1	-1
0-2	-3
0-3	-5
1-2	-1
1-3	-3
2-3	-1

Table 1

Suppose the better ranking player A has a ranking of R_A before the match and the other player B has a ranking of R_B.

The ranking difference is:-

Rank_Diff = R_B – R_A

Rank_Diff is then limited to be in the range -10 to +10.  This is designed to avoid extreme changes of ranking when comparing players of very different abilities.

The most likely ranking difference based on the match result is taken from Table 1

Rank_Delta = Rank_Deltas(GamesA, GamesB)

where GamesA is the number of games won by player A and GamesB is the number of games won by player B

Next we calculate what the error is in the current ranking difference

If Match_Score = “3-0” and Rank_Diff > 5 Then

‘Do nothing, since the match went according to expectation

Rank_Error = 0

Else

Rank_Error = Rank_Delta - Rank_Diff

End If

Then we adjust the player rankings to reduce the error, using a suitable weighting factor in order to smooth the changes.  If one of the players has a provisional ranking (and the other doesn’t), then only the provisional player’s ranking is adjusted.

If both players have an established ranking Then

Delta = 0.25 * Rank_Error

R_A = R_A – Delta

R_B = R_B + Delta

ElseIf both player have a provisional ranking Then

Delta = 0.5 * Rank_Error

R_A = R_A – Delta

R_B = R_B + Delta

ElseIf Player A has a provisional ranking Then

Delta = 0.5 * Rank_Error

R_A = R_A – Delta

ElseIf Player B has a provisional ranking Then

Delta = 0.5 * Rank_Error

R_B = R_B + Delta

End If

 

Let’s look at a concrete example of two players with an established ranking.

R_A = 22

R_B = 27

Match score is 3-2 to player A

Rank_Diff = 5

Rank_Delta = 1

Rank_Error = Rank_Delta – Rank_Diff = -4

Delta = 0.25 * Rank_Error = -1

Therefore, the ranking of player A is increased (worsened) to 23, and the ranking of player B is decreased (improved) to 26.  This is despite the fact that Player A actually won the match 3-2.  The logic behind this, is that with a handicap difference of 5, Player A should be expected to win the match 3-0.

Taking another example.

R_A = 22

R_B = 23

Match score is 3-0 to player A

Rank_Diff = 1

Rank_Delta = 5

Rank_Error = Rank_Delta – Rank_Diff = +4

Delta = 0.25 * Rank_Error = +1

Therefore, the ranking of player A is decreased (improved) to 21, and the ranking of player B is increased (worsened) to 24.  This is because Player A was expected to win the match 3-2, but actually won the match 3-0.

Handicapped Competitions

For a handicapped competition, if the handicaps are correct, then we would expect each match to end in a draw, or at least be very close.

From Figure 1, we can calculate the probability of the better player winning each point based on the handicap difference between the two players.  Suppose the probability is P_A.

For an American 25 point competition match, we would expect players of equal ranking to start at 0-0 and to play a total of 50 points per game.  So, setting the total number of points that we want to be played per game to 50, then player A will win a total of 50 * P_A points and player B will win a total of 50 * (1-P_A) points.  So to achieve a draw, player A should start on 25 – 50 * P_A points and player B should start on 25 – 50 * (1-P_A) points.

Plotting this:-

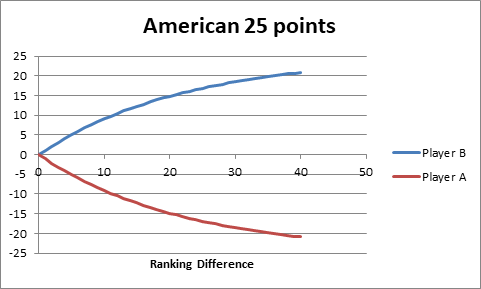
Figure 5

Similarly for an American 15 point tournament.

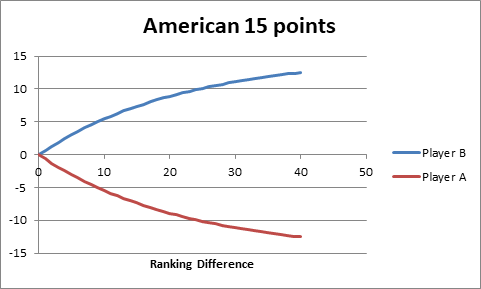
Figure 6

Ideally, following each handicapped tournament match, we would use the number of points won by each player in order to adjust the handicaps suitably.  However, since the game scores aren’t normally recorded, just the overall match result, it is proposed to adjust the player handicaps by 1 for each match played depending on the result ie. the winner’s handicap will be decreased (improved) by 1 and the loser’s handicap will be increased (worsened) by 1.

Assuming that there are 4 rounds in the competition, the overall winner will therefore have their handicap improved by 4, thus decreasing the likelihood that they will win the competition next time.

At the moment, these handicap adjustments will be made manually after the end of the completion, whereas the handicap adjustments made as a result of league matches will be made automatically when the leagues are processed at the end of each month.  At some point, we may automate the competition handicap adjustments as well.

Questions

Q)           I won all of my league matches and yet my handicap has worsened.  How is this possible?

A)           This is unusual, however if your handicap is such that you are expected to beat your opponents convincingly and you only win your matches by small margins, then your handicap might suffer.

Q)           Wouldn’t it be better to actually use the points scored each game in order to adjust the handicaps.

A)           Yes, quite possibly.  However this would require significant changes to the website and leagues application software in order to allow points each games recorded.  Besides which, it might also be difficult to remember the points scored each game unless they are recorded immediately.  The new system of using the games scored should at least represent a significant improvement over the old system.

Q)           What constitutes a provisional ranking.

A)           When a new player enters the ranking system they are given a provisional ranking.  The provisional status indicates that there is a high level of uncertainty about their actual ranking.  Once a player has played in the leagues for 2 months and their results are ‘normal’ ie. they don’t win/lose most of their matches 3-0, then their ranking becomes established.